EQUAÇÃO DE GRACELI.. PARA INTERAÇÕES DE ONDAS E INTERAÇÕES DAS FORÇAS FUNDAMENTAIS.

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

1 / G* =  = [          ] ω  , ,  / T] / c [    [x,t] ] [-1] = 

G* = = OPERADOR DE GRACELI = Em mecânica quântica, o OPERADOR DE GRACELI [ G* =]  é um operador cujo observável corresponde à  ENERGIA TOTAL DO SISTEMA , TODAS AS INTERAÇÕES INCLUINDO TODAS AS INTERAÇÕES DAS FORÇAS FUNDAMENTAIS [AS QUATRO FORÇAS] [ELETROMAGNÉTICA, FORTE, FRACA E GRAVITACIONAL], INTERAÇÕES SPINS-ÓRBITAS, ESTRUTURRA ELETRÔNICA DOS ELEMENTOS QUÍMICOS, TRANSFORMAÇÕES, SISTEMAS DE ONDAS QUÂNTICAS, MOMENTUM MAGNÉTICO de cada elemento químico e partícula, NÍVEIS DE ENERGIA , número quântico , e o  sistema GENERALIZADO GRACELI.

COMO TAMBÉM ESTÁ RELACIONADO A TODO SISTEMA CATEGORIAL GRACELI, TENSORIAL GRACELI DIMENSIONAL DE GRACELI..

Em física, a dispersão de Rutherford é um fenômeno que foi explicado por Ernest Rutherford em 1909,^[1] e levou ao desenvolvimento da teoria orbital do átomo. É agora explorado pela técnica de análise de materiais espectrometria de dispersão de Rutherford. A dispersão de Rutherford é também referida às vezes como dispersão de Coulomb porque baseia-se em forças eletrostáticas (Coulomb). Um processo similar provou o interior do núcleo nos anos 1960, chamado dispersão profunda inelástica.

Destaques da experiência de Rutherford

• Um feixe de partículas alfa é direcionado a uma folha de ouro fina.
• Muitas das partículas passaram através da película sem sofrer desvio.
• Outras foram desviadas por diversos ângulos.
• Algumas inverteram o sentido do movimento.

A partir destes resultados, Rutherford concluiu que a maioria da massa era concentrada numa região minúscula, positivamente carregada (o núcleo), rodeada por electrões. Quando uma partícula alfa (positiva) se aproximava o suficiente do núcleo, era fortemente repelida.^[2] O pequeno tamanho do núcleo explicou a pequena quantidade de partículas alfa que foram repelidas em ângulos maiores. Rutherford demonstrou usando o método abaixo, que o tamanho do núcleo era inferior do que cerca de ${\displaystyle \scriptstyle 10^{-14}}$

Teoria de Dispersão

Geometria de dispersão de Rutherford.

Principais pressupostos:

• Colisão entre uma carga pontual, mais um núcleo pesado com carga Q=Ze é um projétil leve com carga q=ze é considerada como sendo elástica.

• Momento e energia são conservados.

• As partículas interagem através da força de Coulomb.

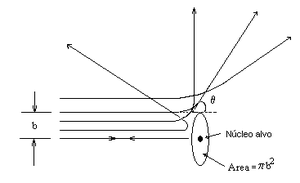
• A distância vertical onde o projétil se encontra a partir do centro do alvo, o parâmetro de impacto b , determinam o ângulo de dispersão θ.

A relação entre o ângulo de dispersão θ, a energia cinética inicial

${\displaystyle E=z{\frac {1}{2}}m.v_{o}^{2}}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

e o parâmetro de impacto b é dado pela relação

${\displaystyle b={\frac {zZ}{2K}}.{\frac {e^{2}}{4\pi \varepsilon _{o}}}{\text{cot}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}$ (1,1)

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

onde z = 2, para partículas-α e Z = 79 de ouro.

Dedução da Transversal Diferencial

Na Figura , uma partícula que atinge o anel entre b e b + db é desviada num ângulo sólido dΩ entre θ e θ + dθ.

Por definição, a secção transversal é a constante de proporcionalidade

${\displaystyle 2\pi b.db=-\sigma (\theta ).2\pi .\operatorname {sen} \theta .d\theta }$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

então

${\displaystyle d\sigma =2\pi b|db|={\Bigg (}{\frac {d\sigma }{d\Omega }}{\Bigg )}.d\Omega }$ (1,2)

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

onde ${\displaystyle d\Omega =2\pi .\operatorname {sen} \theta .d\theta }$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

A seção transversal diferencial torna-se então

${\displaystyle {\frac {d\sigma }{d\Omega }}={\frac {2\pi b|db|}{2\pi .\operatorname {sen} \theta .d\theta }}}$ (1,3)

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

A partir da Equações 1,1 e 1,3 nós temos

${\displaystyle {\frac {d\sigma }{d\Omega }}={\Bigg (}{\frac {1}{4\pi \varepsilon _{o}}}{\Bigg )}^{2}{\Bigg (}{\frac {qQ}{4K_{\alpha }}}{\Bigg )}^{2}.{\frac {1}{\operatorname {sen} ^{4}}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}$ (1.4)

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

A Eq.1.4, é chamada seção transversal diferencial para a dispersão de Rutherford.

Nos cálculos acima, considera-se apenas uma única partícula alfa. Num experimento de dispersão, é preciso considerar vários eventos de dispersão e medir-se a fracção de partículas desviadas num determinado ângulo.

Para um detector em um ângulo específico em relação ao feixe incidente, o número de partículas por unidade de superfície, colidindo o detector, é dado pela fórmula de Rutherford:

${\displaystyle N(\theta )={\frac {N_{i}.nLZ^{2}k^{2}.e^{4}}{4.r^{2}k.E^{2}\operatorname {sen} ^{4}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}}}$

/

 

Verificação da fórmula de Rutherford

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

Onde:

Ni = número de partículas alfa incidentes;

n = átomos por unidade de volume no alvo;

L = espessura do alvo;

Z = número atómico do alvo;

e = carga electrónica;

k = constante de Coulomb;

r = distância entre o alvo e o detector;

KE = energia cinética das partículas alfa;

θ = ângulo de dispersão.

A variação prevista, de partículas alfa detectadas, com ângulo é seguida de perto podados do contador de Geiger-Marsden, mostrados na Figura abaixo.

Cálculo do tamanho nuclear máximo

Espalhamento com diferentes parâmetros de impacto.

Para colisões frontais cabeças entre partículas alfa e o núcleo, toda a energia cinética ${\displaystyle \scriptstyle E=z{\frac {1}{2}}m.v_{o}^{2}}$ da partícula alfa é transformada em energia potencial e a partícula está em repouso.

A distância entre o centro da partícula alfa e o centro do núcleo (b) neste momento é um valor máximo para o raio, se é evidente a partir da experiência que as partículas não atingiram o núcleo.

Aplicando a energia potencial de Coulomb entre as cargas nos electrões e no núcleo, pode-se escrever:

${\displaystyle {\frac {1}{2}}.m.v^{2}={\frac {1}{4\pi \varepsilon _{o}}}.{\frac {q_{1}q_{2}}{b}}}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

Reorganizando,

${\displaystyle {\frac {1}{4\pi \varepsilon _{o}}}{\frac {2.q_{1}q_{2}}{m.v^{2}}}}$ (1,6)

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

Para uma partícula alfa:

• ${\displaystyle m\;({\text{massa}})=6,7\times 10^{-27}\;kg}$
• ${\displaystyle q_{1}=2\times (1,6\times 10^{-19})C}$
• ${\displaystyle q_{2}\;({\text{para ouro}})=79\times (1,6\times 10^{-19})C}$
• ${\displaystyle v_{\;}({\text{velocidade inicial}})=2\times 10^{7}m/s}$

Substituindo estes valores na eqn.1,6, dá o valor do parâmetro de impacto de cerca de ${\displaystyle \scriptstyle 2,7\times 10^{14}m}$ .

O verdadeiro raio é cerca de ${\displaystyle \scriptstyle 7\times 10^{-15}m}$.

Uma colisão de Coulomb é uma colisão elástica binária entre duas partículas carregadas interagindo através de seu próprio campo elétrico. Como com qualquer lei do inverso do quadrado, as trajetórias resultantes das partículas em colisão é uma órbita Kepleriana hiperbólica. Este tipo de colisão é comum em plasmas onde a energia cinética típica das pertículas é grande o suficiente para produzir um desvio significativo das trajetórias iniciais das partículas em colisão, e o efeito cumulativo de muitas colisões é considerado como alternativa.

Tratamento matemático para plasmas

Em um plasma uma colisão de Coulomb raramente resulta em uma grande deflexão. O efeito acumulativo de muitas pequenas colisões, entretanto, é muitas vezes maior que o efeito das poucas colisões de grande ângulo, portanto, é instrutivo considerar a dinâmica da colisão no limite das pequenas deflexões.

Pode-se considerar um elétron de carga -e e massa m_e passando um íon estacionário de carga +Ze e muito maior massa a uma distância b com uma velocidade v. A força perpendicular é (1/4πε₀)Ze²/b² na maior aproximação e a duração do encontro é sobre b/v. O produto destas expressões dividida pela massa é a carga em velocidade perpendicular:

${\displaystyle \Delta m_{e}v_{\perp }\approx {\frac {Ze^{2}}{4\pi \epsilon _{0}}}\,{\frac {1}{vb}}}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

Em matemática e física, teoria da dispersão ou espalhamento é um campo para o estudo e entendimento do espalhamento de ondas e partículas. Espalhamento de ondas corresponde à colisão e espalhamento de uma onda com algum objeto material, por exemplo luz solar espalhada por gotas de chuva para a formação de um arco-íris. Espalhamento também inclui a interação de bolas de bilhar numa mesa, o espalhamento Rutherford (ou mudança de ângulo) de partículas alfa por núcleos de ouro, o espalhamento (ou difração) de Bragg de elétrons e raios X por um grupo de átomos, e o espalhamento inelástico de um fragmento de fissão nuclear que atravessa uma lâmina fina. Mais precisamente, o espalhamento consiste no estudo de como soluções de equações diferenciais parciais, propagando livremente num "passado distante", se juntam e interagem umas com as outras ou com uma condição de contorno, e então propagam-se para um "futuro distante". O "problema de espalhamento direto" é o problema de determinar a distribuição da radiação espalhada (ou fluxo de partículas espalhadas) baseadas na características do centro espalhador. O problema inverso de espalhamento é o problema na determinação das características de um objeto (como por exemplo, sua forma, constituição interna) a partir de dados medidos de radiação ou partículas espalhadas pelo objeto.

Desde sua primeira enunciação para radiolocalização, o problema encontrou um vasto número de aplicações, tais como ecolocalização, pesquisas geofísicas, testes não destritivos, imagens médicas e na teoria quântica de campos, para mencionar alguns.

Base conceitual

Os conceitos usados na teoria de espalhamento têm diferentes nomes em diferentes campos. O objetivo dessa sessão é apontar ao leitor alguns termos comuns.

Alvos compostos e equações de alcance

Quantidades equivalentes usadas na teoria de espalhamento de espécimes compostos, mas com uma variedade de unidades.

Quando um alvo é um conjunto de vários centros espalhadores cujas posições relativas variam de forma imprevisível, é costumeiro que se pense em uma equação de alcance cujos argumentos tomem diferentes formas em diferentes áreas de aplicação. O caso mais simples considera uma interação que remove partículas de um "feixe não espalhado" a uma taxa uniforme que é proporcional ao fluxo incidente ${\displaystyle I}$ de partículas por unidade de área por unidade de tempo, ou seja, que

${\displaystyle {\frac {dI}{dx}}=-QI\,\!}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

onde "Q" é um coeficiente de interação e "x" é a distância viajada no alvo.

A equação diferencial ordinária de primeira ordem acima tem soluções da forma:

${\displaystyle I=I_{o}e^{-Q\Delta x}=I_{o}e^{-{\frac {\Delta x}{\lambda }}}=I_{o}e^{-\sigma (\eta \Delta x)}=I_{o}e^{-{\frac {\rho \Delta x}{\tau }}},}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

onde I_o é o fluxo inicial, comprimento de caminho Δx ≡ x − x_o, a segunda igualdade define uma interação de livre caminho médio λ, a terceira usa o número de alvos por unidade de volume, η, para definir uma área de seção de choque σ, e a última usa a densidade de massa do alvo, ρ, para definir uma densidade de livre caminho médio, τ. Dessa forma, podemos relacionar essas quantidades por meio de Q = 1/λ = ησ = ρ/τ, como mostrada na figura à esquerda.

Em espectroscopia de absorção eletromagnética, por exemplo, o coeficiente de interação (ou seja, Q em cm⁻¹) é comumente chamado de opacidade, coeficiente de absorção e coeficiente de atenuação. Em física nuclear, seções de choque (ou seja, σ em barns ou unidades de 10⁻²⁴ cm²), densidade de livre caminho médio (ou seja, τ em gramas/cm²), e seu recíproco, o coeficiente de atenuação de massa (em cm²/gram) ou "área por nucleon" são todos populares, enquanto em microscopia eletrônica o livre caminho médio inelástico ^[1] (ou seja, λ em nanômetros) é frequentemente discutido^[2] ao invés dos outros.

Fórmula da variação de Compton

Compton usou uma combinação de três fundamentais fórmulas representando os diversos aspectos da física clássica e moderna, combinando-os para descrever o procedimento quântico da luz^[3].

• Luz como uma partícula;
• Dinâmica Relativística;
• Trigonometria.

O resultado final nos dá a equação do espalhamento de Compton:

${\displaystyle \lambda -\lambda _{0}={\frac {h}{m_{e}c}}(1-\cos {\theta })}$

/

G* =  = [          ] ω  , ,  / T]  / c [    [x,t] ]  = 

Onde:

${\displaystyle \lambda _{0}}$ é o comprimento de onda do fóton antes do espalhamento,

${\displaystyle \lambda }$ é o comprimento de onda do fóton depois do espalhamento,

m_e é a massa do elétron,

${\displaystyle {\frac {h}{m_{e}c}}}$ é conhecido como o comprimento de onda de Compton,

θ é o ângulo pelo qual a direção do fóton muda,

h é a constante de Planck, e

c é a velocidade da luz no vácuo.

Coletivamente, o comprimento de onda de Compton é ${\displaystyle 2,43\times 10^{-12}m}$.